La soluzione di:    d f(x) / dx  =  g(x),   f(a) = k

Dal grafico della velocità in funzione del tempo posso risalire al grafico della strada percorsa in funzione del tempo?

A fianco il grafico della velocità v (m/s) in funzione del tempo t (s) di un'automobile.  Per 3 s viaggia a 10 m/s.  Per altri 2 s la velocità aumenta fino ad arrivare a 50 m/s.  Poi la velocità scende per altri 5 s fino a fermarsi. La velocità è  d S(t) / dt  dove S(t) sono i metri di strada percorsa dopo t secondi. Sotto il grafico della posizione dell'auto lungo la strada S (m) in funzione del tempo trascorso t (s).  Nei primi tre secondi la velocità costante corrisponde ad una crescita lineare della strada percorsa.  Nei successivi due secondi la velocità cresce linearmente: ciò in corrispondenza ad una crescita quadratica della strada percorsa; infatti la derivata di una funzione di t che cresce come k·t² è la funzione 2·k·t.  In altri 5 s la velocità scende linearmente, in corrispondenza ancora di un andamento quadratico della strada percorsa, ma il cui grafico è una parabola questa volta con la concavità rivolta in basso.  Infine l'ultimo tratto con velocità nulla corrisponde ad una posizione costante dell'auto.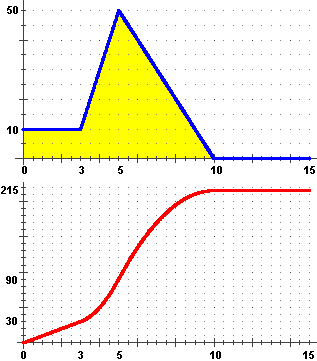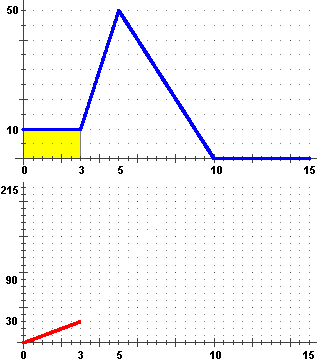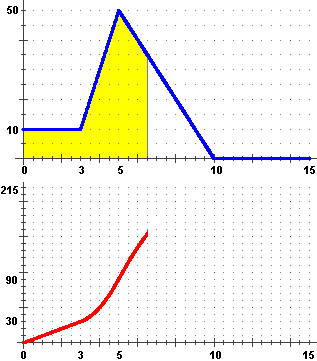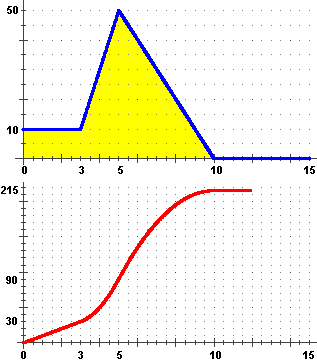

In pratica l'area gialla sotto al grafico blu cresce come il grafico rosso. Possiamo dire che il grafico rosso di S rappresenta la soluzione dell'equazione  d S(t) / d t  nell'ipotesi che all'inizio (all'istante t = 0) l'auto fosse all'inizio della strada, ovvero che S(0) = 0. Se l'auto fosse partita 40 m più avanti, ossia nel caso in cui S(0) = 40, avremmo il grafico verde rappresentato a fianco. Se fosse partita 40 m prima, ossia nel caso in cui S(0) = -40, avremmo il grafico viola.
		Analogamente, a sinistra ho il grafico di una funzione g e quello di f tale che f ' = g nei casi in cui  f(a) = k1, f(a) = k2, f(a) = k3. Si dice, in tutti questi casi, che f è una antiderivata di g, con un origine evidente di questa denominazione. Vedrai che c'è un teorema, chiamato "teorema fondamentale dell'analisi", che afferma che  ∫ [c,d] g = f(d) - f(c)  se  f ' = g.

Questo teorema consente di calcolare, in molti casi, gli integrali su intervalli di una funzione in modo più rapido rispetto al calcolo nuerico.  Esso è anche all'origine della buffa denominazione di integrale indefinito al posto di antiderivata  (denominazione dovuta al fatto che fino al 1970 non si disponeva di semplici mezzi di calcolo come gli attuali che consentissero di calcolare velocemente gli integrali: si ricorreva tutte le volte che si poteva all'antiderivazione).